Відповідь:
A) Якщо бісектриси від основи і вершини: 68° 44° 68°
Б) Якщо бісектриси від кутів при основі: 56° 68° 56°
Пояснення:
Привіт! Зараз ми швидко усе запишемо:
Дано: Один із кутів, утворених при перетині бісектрис Двох кутів рівнобедреного трикутника, дорівнює 124° . Знайдіть кути трикутника. Скільки розв'язків має задача?
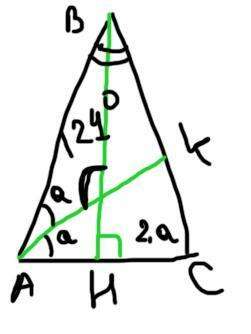
А) Нехай даний трикутник ABC, AB=BC, AK i BH - бісектриси кутів. O-точка перетину цих бісектрис. ∠ВАК=САК=а. Тоді ВСА=2а, бо кути при основі рівнобедреного трикутника рівні, а ∠ВНК=90° (Бо бісектриса=висота - це ознака рівнобедреного трикутника). У ∆ОАН сума суміжних кутів:
∠АОН=180°-124°=56° , а з суми кутів трикутника ∠ОАН=180*-90°-56*=34°.
∠А=∠С=2•34*=68°. З суми кутів трикутника знайдемо: ∠В=180°-2•68°=44°.
Кути трикутника ABC: 68° . 44° . 68°
P.S. Кривий малюнок, але раптом знадобиться :)
Б) Нехай тепер бісектриси йдуть від кутів при основі й утворюють 124°
Отже, з новоствореного трикутника (бісектрисами і основою) з суми кутів трикутника: ∠BAO=∠AOB=(180-124)/2=28°
"Половинки" кутів при основі дорівнюють 28°, тому цілий кут при основі дорівнює 28*2=56°
З суми кутів трикутника ABC, ∠B=180-56*2=68°
Кути трикутника ABC: 56° . 68° . 56°
Готово! Є питання? Запитуйте, з радістю відповім
*Поставте найкраще, будь ласка :)