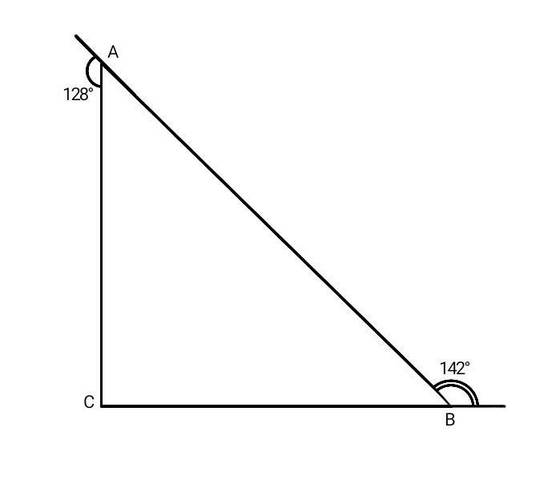
Дано:
∆АВС.
Внешний угол А = 128°.
Внешний угол В = 142°.
Доказать:
∆АВС - прямоугольный.
Доказательство:
Угол САВ = 180°-128° = 52° (так как они смежные).
Угол АВС = 180°-142° = 38° (так как они тоже смежные).
Угол САВ+ угол АВС = 52°+38° = 90°.
А если сумма двух углов треугольника равна 90° , то такой треугольник - прямоугольный. => ∆АВС - прямоугольный.
Ответ: что требовалось доказать.