2 вариант
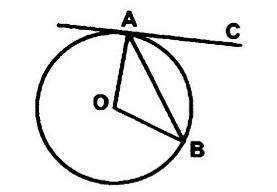
1. СА – касательная к окружности. Вычислите градусную меру угла АВО, если ∠ВАС=44°. [3] 2. Равнобедренный треугольник АВС (АC=CВ) вписан в окружность с центром в точке О. Найдите величины дуг АС, АВ и ВС, если ∠АОВ=100°. [4]3. В окружности с центром в точке О проведен диаметр MN=14 см и хорда CD, перпендикулярная MN и равная радиусу данной окружности. Диаметр MN и хорда CD пересекаются в точке K.a) выполните чертеж по условию задачи;b) найдите радиус окружности; [4]c) найдите длину отрезка CK;d) вычислите периметр треугольника CОD 4. Найдите радиусы двух касающихся окружностей, если они пропорциональны числам 7 и 5, а расстояние между центрами окружностей равно 24 см. Рассмотрите два варианта. [4] 5. Постройте треугольник по сторонам AB=5 см, ВС=7 см и углу ∠АВС = 50о. В полученном треугольнике постройте серединный перпендикуляр к стороне АС. эта картинка относится к 1 заданию