Ответ:
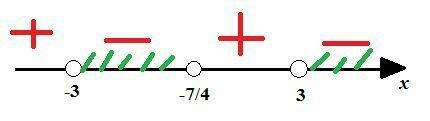
x ∈ (-3 ; -7/4)∨(3 ; +∞)
Объяснение:
Для начала найдем ОДЗ (область допустимых значений):

Когда "решили" знаменатель, находим корни числителя, приравнивая его к нулю:

Теперь отмечаем полученные корни x₁,₂,₃ на координатной прямой. Все точки выколотые (т.е. пустые кружочки, т.к. строгого равенства нет).
Далее нужно расставить знаки функции на интервалах. Для начала возьмем самый правый участок (где 3 и правее). Берем любое число из этого интервала, подставляем в функцию и проверяем знак. Например, возьмем 4:

Получили отрицательное значение, значит, на этом интервале функция принимает отрицательные значения - ставим минус.
Далее есть правило: при переходе между интервалами функция меняет знак. Т.е. дальше ставим чередованием плюса и минуса.
И выделяем лишь те интервалы, где функция меньше нуля - отрицательная.
Вот и все.