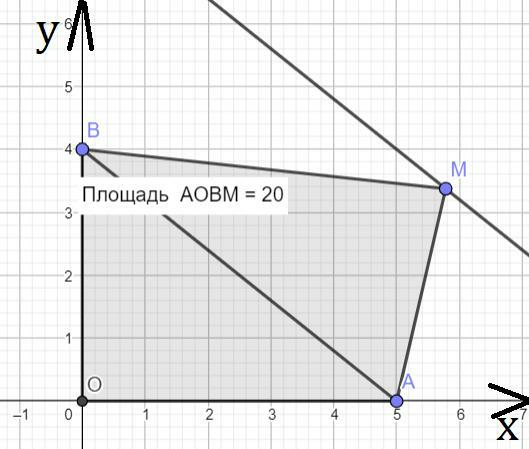
Прямая проходящая через точки A, B имеет уравнение:
y=ax+t, подставим координаты точек чтобы найти уравнение в явном виде.
4=a·o+t ⇒ t=4; 0=a·5+t ⇒ a=-4/5=-0,8
Исходя из последовательности вершин четырёхугольника, получаем, что координаты M(x;y) удовлетворяют неравенству y≥-0,8x+4.
Заметим, что S(AOBM) = S(AOB)+S(BMA), при этом S(AOBM)=20, S(AOB)=AO·OB/2=10.
Тогда S(BMA)=10.
Поскольку площадь треугольника постоянная и длина стороны AB тоже. То высота опущенная из M на AB должна быть постоянной, откуда M лежит на прямой параллельной AB. Тогда угол наклона k равен углу наклона прямой проходящей через точки A, B.
k = -0,8
Ответ: -0,8.