Ответ:
Розв'язків немає.
Объяснение:
1) Графічний метод:

Нехай у=2+х - [1], a у=2,5+х - [2].
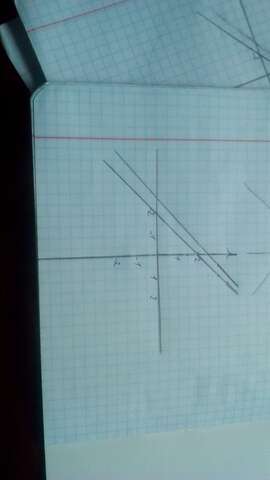
Побудуємо графік і координати для [1]:
х=0, у=2;
х=-2, у=0.
Побудуємо координати для [2]:
х=0, у=2,5;
х=0,5, у=3.
Бачимо, що графіки не перетинаються, або паралельні. Отже, розв'язків немає.
2) Метод підстановки.

Нехай у=2+х - [1], a у=2,5+х - [2].
Підставимо [1] у [2]:
2(2+х)-2х=5;
;4+2х-2х=5;
0х=9;
х=∅.
Порожня множина, отже, розв'язків немає.