1.
Диаметр в окружности всегда равен двум радиусам.
Обозначения: D - диаметр, r - радиус.
A) D=2r=r+r
D=r+40 Следовательно 40=r
D=2r=2*40=80 мм = 8 см
Ответ: диаметр равен 8 см.
B) Если r/2 = 2 см, то r = 2*2 = 4 см
D=2r=2*4=8 см
Ответ: диаметр равен 8 см.
С) Раз окружности равны, то и радиусы, и диаметры в них тоже равны.
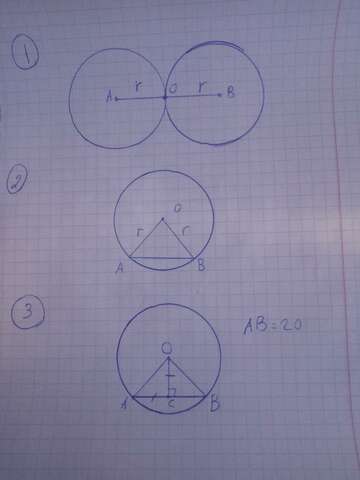
Значит AO=OB=r (см. рисунок).
AO+OB=2r=AB=D
D=AB=4 см
Ответ: диаметр равен 4 см.
2.
OA=OB (т.к. оба радиусы), а AB=OA, значит
OA=OB=AB - все стороны треугольника OAB равны, значит этот треугольник - равносторонний и все углы в нём равны 60° и ∠OBA в том числе.
Ответ: ∠OBA=60°
3.
∠AOC=90°-∠OAB=90-45=45°
∠AOC=∠OAB, значит треугольник OAC - равнобедренный (OC=AC)
ΔOAC=ΔOAB (OC-общ., OA=OB - радиусы), значит AC=BC=20:2=10 см.
OC=AC=10 см
Ответ: длина перпендикуляра равна 10 см.