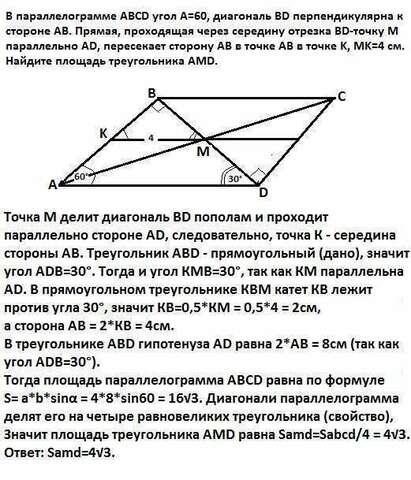
Точка М делит диагональ ВD пополам и проходит параллельно стороне AD, следовательно, точка К - середина стороны АВ. Треугольник АВD - прямоугольный (дано), значит угол АDВ=30°. Тогда и угол КМВ=30°, так как КМ параллельна АD. В прямоугольном треугольнике КВМ катет КВ лежит против угла 30°, значит КВ=0,5*КМ = 0,5*4 = 2см, а сторона АВ = 2*КВ = 4см.
В треугольнике АВD гипотенуза AD равна 2*АВ = 8см (так как угол АDВ=30°).
Тогда площадь параллелограмма АВСD равна по формуле S= a*b*sinα = 4*8*sin60 = 16√3. Диагонали параллелограмма делят его на четыре равновеликих треугольника (свойство), Значит площадь треугольника AMD равна Samd=Sabcd/4 = 4√3.
Ответ: Samd=4√3.