Очевидно, что здесь график будет основан на параболе.
Сейчас посмотрим, что будет при раскрытии модуля
 3} \atop {3-x, x<3}} \right." alt="\displaystyle |x-3| = \left \{ {{x-3,x>3} \atop {3-x, x<3}} \right." align="absmiddle" class="latex-formula">
3} \atop {3-x, x<3}} \right." alt="\displaystyle |x-3| = \left \{ {{x-3,x>3} \atop {3-x, x<3}} \right." align="absmiddle" class="latex-formula">
Не стал рассматривать  , потому что он в знаменателе дроби.
, потому что он в знаменателе дроби.
При положительном раскрытии дробь равна 1, при отрицательном раскрытии дробь равна -1.
Итого имеем:
 3} \atop {x^2-6x-1+3, x<3}} \right." alt="\displaystyle y=\left \{ {{x^2-6x+1+3, x>3} \atop {x^2-6x-1+3, x<3}} \right." align="absmiddle" class="latex-formula">
3} \atop {x^2-6x-1+3, x<3}} \right." alt="\displaystyle y=\left \{ {{x^2-6x+1+3, x>3} \atop {x^2-6x-1+3, x<3}} \right." align="absmiddle" class="latex-formula">
То есть  3} \atop {x^2-6x+2, x<3}} \right." alt="\displaystyle y=\left \{ {{x^2-6x+4, x>3} \atop {x^2-6x+2, x<3}} \right." align="absmiddle" class="latex-formula">
3} \atop {x^2-6x+2, x<3}} \right." alt="\displaystyle y=\left \{ {{x^2-6x+4, x>3} \atop {x^2-6x+2, x<3}} \right." align="absmiddle" class="latex-formula">
Чтобы было удобно строить, выделим полный квадрат и увидим, что оба куска различаются лишь расположением по оси ОУ, а так та же парабола.
 3} \atop {x^2-6x+9-9+2=(x-3)^2-7, x<3}} \right." alt="\displaystyle y=\left \{ {{x^2-6x+9-9+4=(x-3)^2-5, x>3} \atop {x^2-6x+9-9+2=(x-3)^2-7, x<3}} \right." align="absmiddle" class="latex-formula">
3} \atop {x^2-6x+9-9+2=(x-3)^2-7, x<3}} \right." alt="\displaystyle y=\left \{ {{x^2-6x+9-9+4=(x-3)^2-5, x>3} \atop {x^2-6x+9-9+2=(x-3)^2-7, x<3}} \right." align="absmiddle" class="latex-formula">
То есть оба куска смещены по оси ОХ на 3 единицы вправо, а смещение по ОУ зависит от самого куска: левый кусок  смещен на 7 единиц вниз, а правый
смещен на 7 единиц вниз, а правый  3)" alt="(x>3)" align="absmiddle" class="latex-formula"> - на 5 единиц вниз.
3)" alt="(x>3)" align="absmiddle" class="latex-formula"> - на 5 единиц вниз.
Кстати, в  - разрыв, поэтому на графике будут две выколотые точки - слева и справа.
- разрыв, поэтому на графике будут две выколотые точки - слева и справа.
Сам график строится так:
Строятся полностью оба куска (довольно легко, по факту из новой точки - в 1-ом куске (3;-5), во 2-м (3;-7) строим самые простые параболы  , ну то есть мысленно представляем, что, например, точка (3;-5) является началом координат и от неё параболку шаблонную строим с заученной наизусть таблицей) и на каждом интервале остается только та часть, которая указана в системе.
, ну то есть мысленно представляем, что, например, точка (3;-5) является началом координат и от неё параболку шаблонную строим с заученной наизусть таблицей) и на каждом интервале остается только та часть, которая указана в системе.
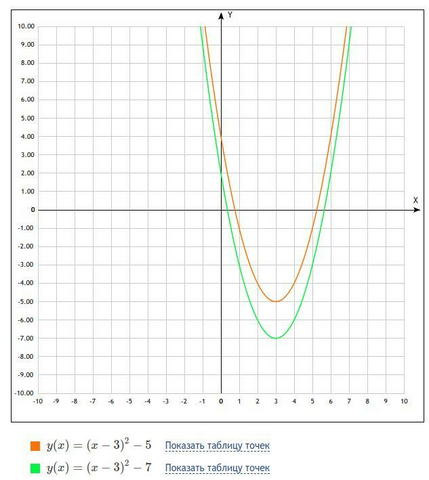
Картинка 1 - два графика разным цветом
Картинка 2 - итоговый график, то есть после того, как ненужные части были убраны и был добавлен разрыв.