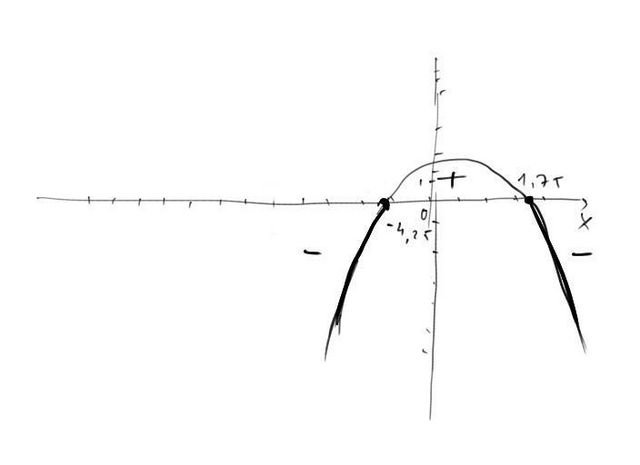
1) Пусть -2x^2-5x+18=y. В точках пересечения параболы с осью X, y = 0, поэтому, чтобы найти координаты этих точек пересечения, приравняем левую часть уравнения к нулю. Получаем:
-2x^2-5x+18=0
D=144
x1=(5+12)/(2*(-2))=-4,25
x2=(5-12)/(2*(-2))=1,75
Итак, в этих точка парабола пересекает ось x
Поскольку коэффициент a(тот что перед x^2)<0, ветви параболы направлены вниз.</p>
Зная это, можем изобразить параболу(прикреп)
Нам нужно найти x при которых y(он же -2x^2-5x+18)<= 0.</p>
Смотрим на рисунок. Y меньше или равен нулю там, где график пересекает ось X и где он под осью X.
Остается определить x для этих частей графика.
X=(-∞;-4,25]∪[1,75;+∞) (квадратные скобки там, т.к. неравенство нестрогое)
2) найдем ОДЗ:
x≠-3
Теперь домножим обе часть на x+3
Если x+3<0(x<-3), то знак поменяется на противоположный, и получим:</p>
6x+1>0
x>-1/6
Чисел, удовлетворяющих условию (x<-3) и (x>-1/6) не существует.
Если x+3>0(x>-3), то знак не изменится, получим:
6x+1<0</p>
x<-1/6</p>
Значит, x лежит в пределах (-3; -1/6). Наименьшее целое число из этого интервала это -2.
Ответ: -2
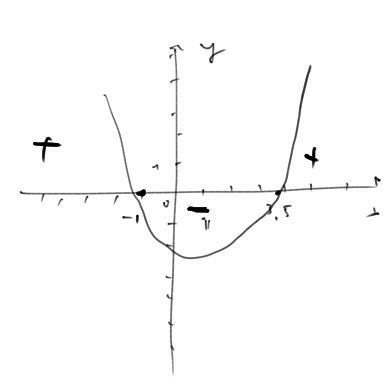
3) Воспользуемся тем же алгоритмом, что и в первом задании. Найдем точки пересечения графика параболы:
D=81
x1=(5+9)/(2*2)=3,5
x2=x1=(5-9)/(2*2)=-1
В этих точка парабола пересекает ось x
Поскольку коэффициент a(тот что перед x^2)>0, ветви параболы направлены вверх.
Зная это, можем изобразить параболу(прикреп2)
Нам нужно найти x при которых y(он же 2x^2-5x-7)>= 0.
Смотрим на рисунок. Y больше или равен нулю там, где график пересекает ось X и где он над осью X.
Остается определить x для этих частей графика.
X=(-∞;-1]∪[3,5;+∞)
Второе условие для x вытекает из второго неравенства системы:
x -3 >0
x>3
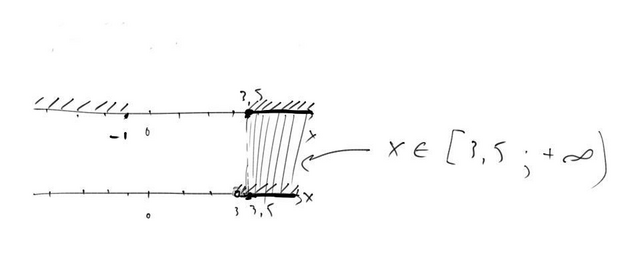
Это можно решить графически(прикреп3)
Разместим эти условия на двух разных координатных прямых(ноль под нулем, единица по единицей и т.д.):
Смотрим на каких промежутках есть x обеих прямых. Это и есть решение.
Видим, что это x ∈[3,5; +∞)