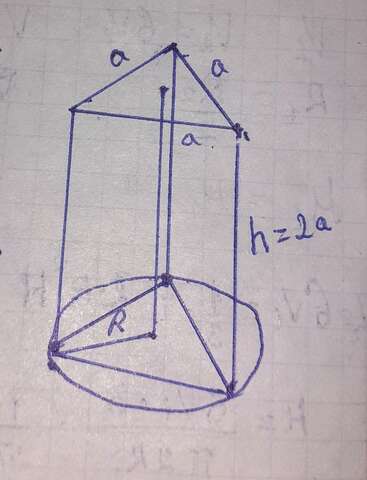
R=3√3 см
Н=2а
Sб.п - ?
на основании правильной треугольной призмы лежит равносторонний треугольник
радиус описанной около равностороннего треугольника
R=a/√3 отсюда сторона треугольника
а=R×√3=3√3 ×√3=9 см
высота Н=2а=2×9=18 см
площадь боковой поверхности призмы
Sб.п=Р×Н=3а×Н=3×9×18= 486 см²
здесь P=3a периметр основания