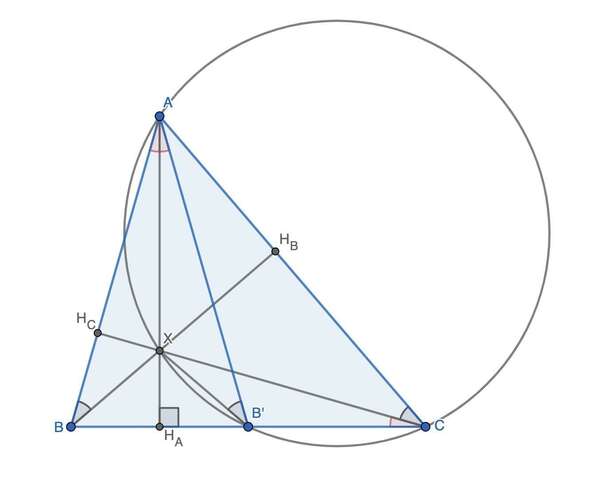
Пусть  — высота. Выполним симметрию ΔABX относительно AX. ΔABX переходит в ΔAB'X. ∠AB'X = ∠ACX и опираются на один отрезок, значит, AXB'C — вписанный четырёхугольник. Тогда и ∠B'CX = ∠B'AX. Но ΔBAB' — равнобедренный по построению, где
— высота. Выполним симметрию ΔABX относительно AX. ΔABX переходит в ΔAB'X. ∠AB'X = ∠ACX и опираются на один отрезок, значит, AXB'C — вписанный четырёхугольник. Тогда и ∠B'CX = ∠B'AX. Но ΔBAB' — равнобедренный по построению, где  — высота. Тогда ∠BAX = ∠B'AX = ∠B'CX.
— высота. Тогда ∠BAX = ∠B'AX = ∠B'CX.
Пусть прямая CX пересекает AB в  , а BX пересекает AC — в
, а BX пересекает AC — в  . Рассмотрим
. Рассмотрим  и
и  : ∠B — общий,
: ∠B — общий,  ⇒
⇒  , но
, но  — прямой, тогда и
— прямой, тогда и  — прямой.
— прямой.  — высоты, пересекаются в точке X, тогда
— высоты, пересекаются в точке X, тогда  — также высота, X — ортоцентр, что и требовалось доказать.
— также высота, X — ортоцентр, что и требовалось доказать.