Помогите решить, пожалуйста!

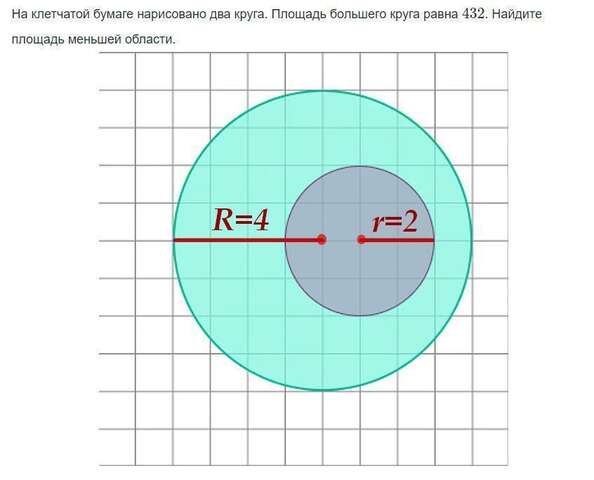
Задача: На клетчатой бумаге нарисовано два круга. Площадь большего круга равна 432. Найдите площадь меньшей области.

Решение:

Отношение площадей фигур равно квадрату их коэффициента подобия.

$\frac{S_1}{S_2}=k^2$

Пусть S₁ = 432 (кв.ед.) — площадь большего круга, тогда S₂ — площадь меньшего, R = 4 (ед.) — радиус большего круга, r (ед.) — радиус меньшего.

Коэффициент подобия будет равен:

$k = \frac{R}{r} = \frac{4}{2} =2$

Подставим значения в исходную формулу:

$\frac{432}{S_2}=2^2 \:\: \Rightarrow \:\: S_2 = \frac{432}{4} = 108$

Ответ: Площадь меньшей области равна 108 кв. ед.