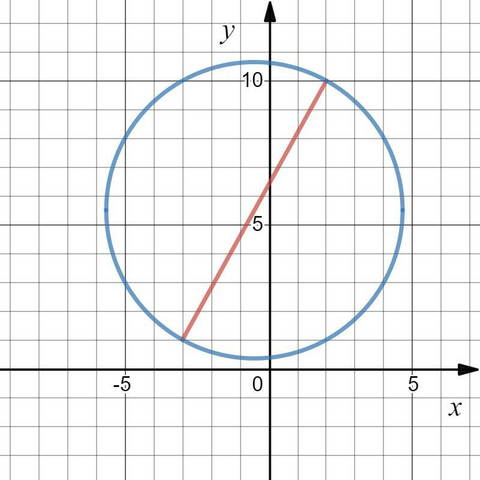
Определим координаты диаметра: 
Определим длину диаметра: 
Тогда радиус окружности 
Определим координаты центра, используя уравнение окружности:

Здесь  , а
, а  и
и  — координаты точек, лежащих на окружности.
— координаты точек, лежащих на окружности.


Вычтем из второго уравнения первое:



Подставим  во второе уравнение:
во второе уравнение:









Тогда 
Следовательно, уравнение окружности:

Окружность изображена на плоскости (см. вложение).