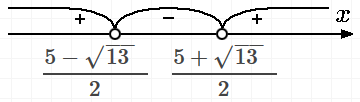Помогите плиз решить неравенство. 1/√(х+1)≥1/(2-х)

$\frac{1}{ \sqrt{(x+1)}}{} \geq \frac{1}{(2-x)}$
$(2-x)} \geq \sqrt{(x+1)$
$(2-x)^2 \geq (x+1)$
$x^{2} -5x+3 \geq 0$
Корни квадратного уравнения
$x_1 = \frac{5-\sqrt{13}}{2} ;\; x_2 = \frac{5+\sqrt{13}}{2}$
Наносим найденные точки на числовую ось и вычисляем знаки на каждом интервале (см. приложение)
решение неравенстава
$x \in \left( -\infty ;\; \frac{5-\sqrt{13}}{2} \right) \cup \left( \frac{5+\sqrt{13}}{2} ;\; +\infty \right)$
или

\frac{5+\sqrt{13}}{2}" alt="x < \frac{5-\sqrt{13}}{2} ;\;\; x > \frac{5+\sqrt{13}}{2}" align="absmiddle" class="latex-formula">

Однако надо учесть ОДЗ:

0 \\ 2-x \neq 0 \end{array}\right." alt="\left\{\begin{array}{l} x+1 > 0 \\ 2-x \neq 0 \end{array}\right." align="absmiddle" class="latex-formula">

-1 \\ x \neq 2 \end{array}\right." alt="\left\{\begin{array}{l} x > -1 \\ x \neq 2 \end{array}\right." align="absmiddle" class="latex-formula">

Ответе:
$x \in \left( -1 ;\; \frac{5-\sqrt{13}}{2} \right) \cup \left( \frac{5+\sqrt{13}}{2} ;\; +\infty \right)$
$x \neq 2$