Высоты, проведённые к боковым сторонам AB и BC равнобедренного треугольника ABC,...

Question

Высоты, проведённые к боковым сторонам AB и BC равнобедренного треугольника ABC, пересекаются в точке M. Прямая BM пересекает основание AC в точке N. Определи ∡CBM, если ∡ABC=52°.

Answer 1

Ответ:

∠CBM=26°.

Объяснение:

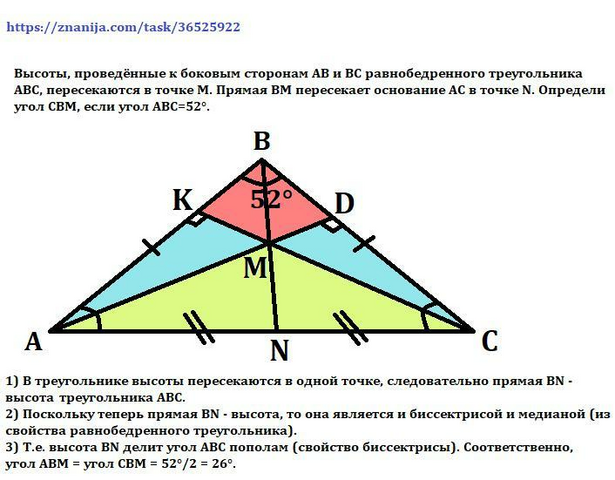
1) В треугольнике высоты пересекаются в одной точке, следовательно прямая BN - высота и треугольника ABC.

2) Поскольку теперь прямая BN - высота, то она является и биссектрисой и медианой (из свойства равнобедренного треугольника).

3) Т.е. высота BN делит ∠ABC пополам (свойство биссектрисы). Соответственно, ∠ABM=∠CBM=52°/2=26°.

---