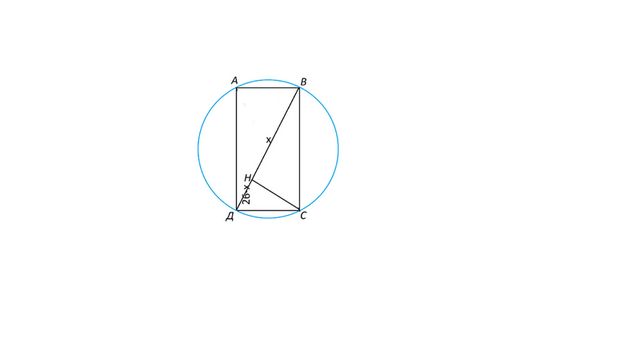
Радиус описанной вокруг прямоугольника окружности равен 13.
Диаметр окружности, следовательно, равен 26, и является диагональю данного по условию прямоугольника.
Обозначим вершины прямоугольника АВСД.
Тогда ВД - его диагональ и делит прямоугольник на два равных прямоугольных треугольника -АВД и ВСД.
Рассмотрим треугольник ВСД.
Гипотенуза равна 13, и вспоминается одна из троек Пифагора с отношением его сторон сторон прямоугольного треугольника 5:12:13. Отношение сторон этого треугольника может быть таким же:
ВС:СД:ВД=5:12:13
Тогда его гипотенуза 26, катеты 10 и 24,
И площадь прямоугольника АВСД= 10*24=240.
Всё сходится.
Но не всегда вспоминаются эти тройки, да и отношение сторон может быть иным.
Решение.
Площадь треугольника ВСД равна половине площади прямоугольника АВСД и равна 120.
Проведем в этом треугольнике высоту СН.
Площадь ВСД=СН*26:2
120*2=СН*26
СН=240/26=120/13
ВС - сторона прямоугольника = катет треугольника ВСН.
Найти его можно из этого треугольника по т.Пифагора.
Для того, чтобы найти ВН, воспользуемся правилом:
Высота прямоугольного треугольника, проведенная из вершины
прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой;
СН²=ВН*НД
(120/13)²=ВН*(26-ВН)
Обозначим ВН=х, тогда НД=26-х
Подставим в уравнение высоты эти значения:
1400/169=26х-х²
Домножим обе части уравнения на 169, чтобы избавиться от дроби:
1400=4394х-169х²
169х²-4394х+14400=0
Решим квадратное уравнение:
Дискриминант равен:
D=b²-4ac=-43942-4·169·14400=9572836
х=(-b±√D):2а
х1=-(-4394)+√9572836):2*169= (4394+3094):338=7288/338=288/13
Второй корень находить нет необходимости.
Найдем катет ВС.
Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой (ВД) и отрезком (ВН) гипотенузы, заключенным между катетом и высотой.
ВС²=ВН²+СН²
ВС²=(288/13)²+(120/13)²
ВС²=576
ВС=24
Из площади прямоугольника найти вторую его сторону не составит труда.
АВ=240:24=10
Периметр прямоугольника
Р=2(АВ+ВС)=2*(24+10)=68