Боковые стороны и меньшее основание трапеции равны 10 см, а один из её углов равен 60...

Question

Боковые стороны и меньшее основание трапеции равны 10 см, а один из её углов равен 60 градусов. Найдите радиус окружности, описанной около этой трапеции.​

Answer 1

Ответ:

10см

Пошаговое объяснение:

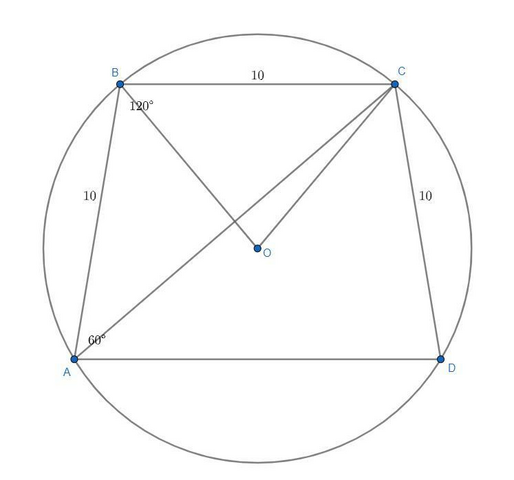
Рассмотрим прикрепленный чертеж. Заметим, что ΔABC - равнобедренный (AB=BC=10 по условию) и ∠ABC=180°-60°=120°. Тогда ∠BAC=(180°-120°)/2=30°. Центральный ∠BOC опирается на ту же дугу, что и вписанный ∠BAC, а значит равен 60°. BO=OC=R и ∠BOC=60° (а значит и два другие угла треугольника равны 60°), поэтому ΔBOC равносторонний. Тогда радиус равен меньшему основанию трапеции, т.е. R=10.

---

Comments

Можно было найти BD по теореме косинусов и, заметив, что треугольник BDC вписан в ту же окружность найти радиус по обобщенной теореме синусов, но я нашел другое решение, которое не требует столь длинных вычислений.

---

спасибо

---

:)