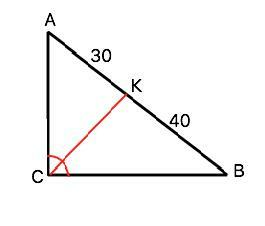
Бисектриса прямого угла прямоугольного треугольника делит гіпотенузу на отрезки 40 см и 30 см. Найдите периметр треугольника.
Решение:
Обозначим треугольник АВС; СК - биссектриса. АК=30 см, ВК=40 см.
Биссектриса угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон. (свойство). АК:ВК=30:40=3:4. =>
АС:ВС=3:4. Из отношения катетов видно, что треугольник АВС - так называемый «египетский» с отношением сторон 3:4:5. .
Примем коэффициент отношения равным а.
Тогда АС=3а, ВС=4а, гипотенуза АВ=5а.
АВ=АВ+ВК=30+40=70 (см) => а=70:5=14(см).
Р=3а+4а+5а=12а
Р=12•14=168 (см)