Пожалуйста, решите подробным решением. И можно ли использовать 5пи/6 и -5пи/6?

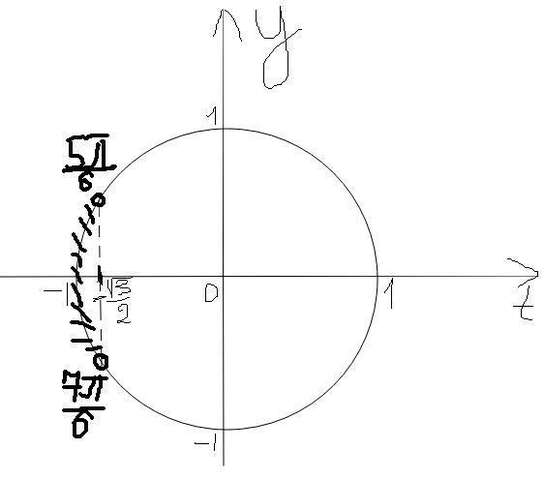
Пусть $\displaystyle t = x+\frac{\pi}{8}$

Рисуем окружность и смотрим, где $\displaystyle cos\ t = -\frac{\sqrt{3} }{2}$ , отмечаем эти точки с одним периодом, это $\displaystyle \frac{5\pi}{6} ; \frac{7\pi}{6}$ .

Косинус меньше будет между этими точками, то есть $\displaystyle \bigg(\frac{5\pi}{6};\frac{7\pi}{6} \bigg)$

Но учитываем, что косинус - функция периодичная, то есть количество таких промежутков бесконечно много и повторяется с периодом $2\pi$ , поэтому в ответ добавляем период