Ответ:
Объяснение: рассмотрим ∆АСД. По условиям угол АДВ=40°, а угол ВДС=10°. Тогда угол Д= 40+10=50°.
Теперь найдём угол САД: Сумма острых углов в прямоугольном треугольнике составляе 90°, поэтому угол САД=90-50=40°. Теперь рассмотрим ∆АОД допустим , что стороны треугольников пересекаются в точке О. Припересечении АС и ВД углы АОД и ВОС равны. Также равны углы АОВ и ДОС. У треугольников АВД и АСД АД общая сторона, которая соединяет АС и ВД. Это треугольник равнобедренный, так как у него углы при основании равны и составляют 40°. Теперь рассмотрим ∆АВД. В нём угол АДВ= 40°, а угол В= 90°. Зная, что сумма острых углов треугольника составляет 90°, найдём угол ВАД. Угол ВАД= 90-40=50°.
Зная что угол САД=40°, а угол ВАД=50°, то угол ВАС= 50-40=10°. Поэтому у треугольников АВД и ДСА угол ВАД=углу СДА; угол В = углу С; угол САД= углу ВДА. Эти треугольники равны по трём углам.
Задание 2:
Пусть угол при основании будет х, тогда угол вершины будет 4х. Зная, что сумма углов треугольника составляет 180°, составим уравнение:
х+х+4х=180
6х=180
х=180÷6
х=30° Итак углы при основании будут по 30°, тогда угол вершины треугольника будет 30×4=120°;
Углы при основании по 30°
Угол вершины=120°
Задание 3
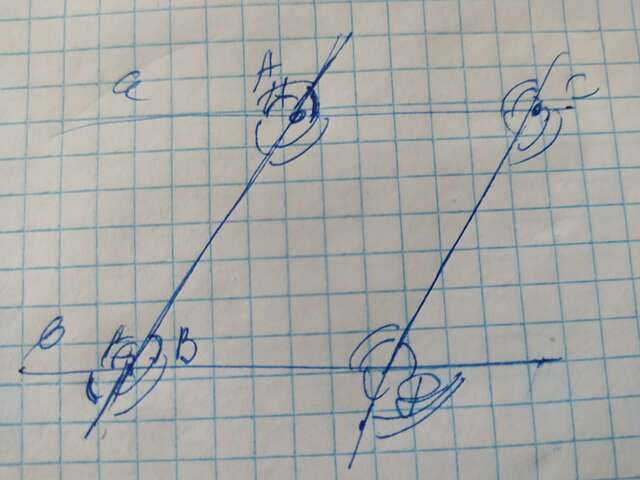
При пересечении двух параллельных прямых и секущей углы внешние односторонние и внутренние односторонние равны. Также две параллельные секущие отсекают от двух других параллельных прямых равные отрезки, поэтому АС =ВД