Глеб расставил числа 1, 5, 7, 8, 11, 12, 13 в вершины и центр правильного шестиугольника...

Question

Глеб расставил числа 1, 5, 7, 8, 11, 12, 13 в вершины и центр правильного шестиугольника так, что в любом из 6 равносторонних треугольников сумма чисел в вершинах делится на 3. Какое число Глеб мог записать в центр? Достаточно привести один подходящий пример.

Answer 1

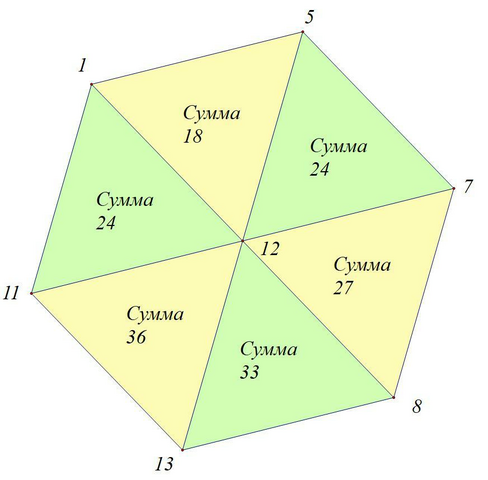
Ответ: 12

Решение во вложении.

Как заполнялось.

Сначала произвольно ставилось число в центр.

Для начала взяли число 12, так как оно делится на 3. Значит надо расставлять по краям такие числа, чтобы при сложении соседних, получалось число, кратное 3.

Произвольно выберем вершину и поставим цифру 1. Тогда надо подобрать такое число (из имеющихся), чтобы (1 + X) делилось на 3.

1 + 5 = 6 -- делится на 3 -- подходит

Ставим число 5 около соседней вершины (решений у задачи много, поэтому может быть и другое число: 11 или 8)

Далее (5 + Х) делится на 3, откуда подходит число 7, записываем его рядом с 5. И далее аналогично:

7 + 8 = 15 -- делится,

8 + 13 = 21 -- делится,

13 + 11 = 24 -- делится,

11 + 1 = 12 -- делится.

---