Выберу ваш ответ ЛУЧШИМ! Помогите решить лишь 1 задание! Известно, что площадь боковой...

Question

Выберу ваш ответ ЛУЧШИМ! Помогите решить лишь 1 задание! Известно, что площадь боковой поверхности правильной n-угольной пирамиды вдвое больше площади ее основания. Найти угол между боковой гранью и основанием пирамиды. Відомо, що площа бічної поверхні правильної n-кутної піраміди вдвічі більша за площу її основи. Визначте кут між бічною гранню та основою піраміди.

Answer 1

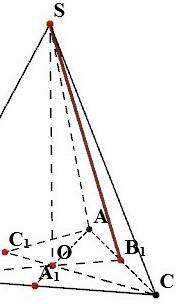
Пусть сторона основания AB = x, высота боковой грани SB1 = y, а высота пирамиды SO = h.

Площадь основания пирамиды S1=(√(3)/4) * x², площадь боковой грани S2= 0,5xy, площадь боковой поверхности S3 = 3 * S2=(3/2)xy.

По условиям задачи S3 = 2 * S1 -> (3/2)xy=2(√(3)/4) * x² -> y=x/√3

Косинус искомого угла a = OB1/SB1 = (0,5xtg(30g))/y = (0,5x(1/√(3))/(x * (1/√(3))), т.е. косинус равен 1/2, а это соответствует углу 60 градусов.

Ответ: 60 градусов.

---

Comments

сори, не смог B поместить на картинку

---

а откуда корень из 3/4?)

---

не корень из 3/4, а корень из трёх деленный на 4

---

я же специально тройку в скобочку засунул

---

это я и имею в виду... откуда эта цифра взялась?

---

это формула вычисления площади основания пирамиды :)

---

(0,5xtg(30g)) ты написал, что это ОВ1, а это по условию разве не SB1? Ведь мы обозначали у= высота боковой грани...

---

Ты не знаешь как находить косинус или что? ОТНОШЕНИЕ ПРОТИВОПОЛОЖНОГО КАТЕТА К ГИПОТЕНУЗЕ => OB1/SB1