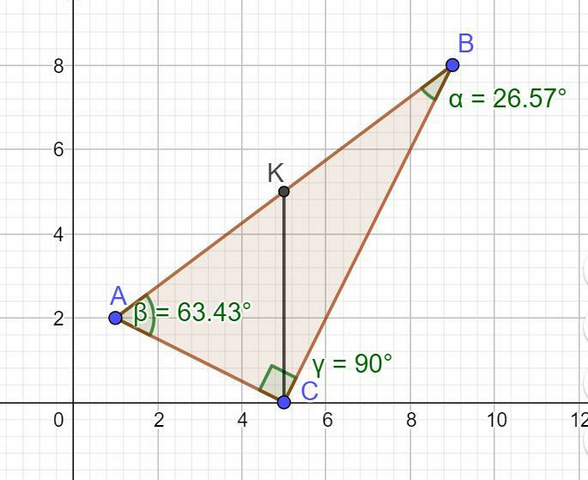
Группа А, вариант 1.
Даны вершины треугольника.
Точка А Точка В Точка С
х у х у х у
1 2 9 8 5 0
Находим длины сторон.
АВ ВС АС
Δx Δy Δx Δy Δx Δy
8 6 -4 -8 4 -2
64 36 16 64 16 4 квадраты
100 80 20 сумма квадратов
АВ (c) = 10 ВС(a) = √80 = 4√5 АС (b) = √20 = 2√5 .
Углы по теореме косинусов:
cos A =0,4472 A =1,107 радиан или63,435 градуса
cos B =0,8944 B =0,4637 радиан или 26,565 градуса
cos C =0 C =1,5708 радиан или 90 градусов.
Как видом, треугольник прямоугольный.
Векторы и модули сторон определились выше:
АВ (8; 6), ВС(-4; -8) АС(4; -2).
10 4√5 2√5
Косинусы углов можно определить по векторам.
Например, cos А = (AB*AC)/(|AB|*|AC|) =
(8*4 + 6*(-2)/(10* 2√5 ) = 20/(20√5 ) = 1/√5 ≈ 0,44721.
Что соответствует ранее найденному.
Уравнения сторон.
АВ: (х - 1)/8 = (у -2)/6 это канонический вид,
6х - 8у + 10 = 0 или 3х - 4у + 5 = 0 это общий вид,
у = (3/4)х + (5/4) вариант с угловым коэффициентом.
ВС: (х - 9)/(-4) = (у -8)/(-8),
АС: (х - 1)/4 = (у -2)/9-2).
Другие варианты можно определить самостоятельно.
Площадь треугольника можно определить или по формуле Герона, или по координатам:
S = (1/2)|(x2 - x1)*(y3 - y1) - (x3 - x1)*(y2 - y1)|.
Подставив значения, получаем S = 20.
Находим координаты точки К - середины стороны АВ:
К = ((1+9)/2=5; (2+8)/2=5) = (5; 5).
Теперь находим вектор СК:
СК = ((5-5)=0; (5-0=5) = (0; 5).
Уравнение медианы СК:
(х - 5)/0 = (у - 0)/5 или х = 5. Это вертикальная линия.