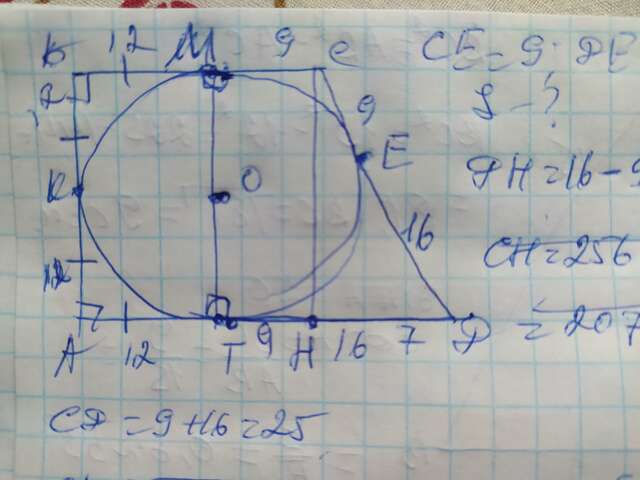
Ответ: S=588см²
Объяснение: Обозначим вершины трапеции А В С Д а точки касания К М Е Т, центр вписанной окружности О. Стороны трапеции являются касательными к вписанной окружности и отрезки касательных соединяясь в одной вершине равны от вершины до точки касания, поэтому: МС=СЕ=9см, ЕД=ДТ=16см. Проведём к основанию АД две высоты СН и МТ, которые равны между собой и равны диаметру окружности. Они делят АД так что ТН=МС=9см, тогда ДН=16-9=7см. Рассмотрим полученный ∆СДН. Он прямоугольный,мгле СД- гипотенуза, а СН и ДН - катеты. СД=9+16=25см.
Найдём СН по теореме Пифагора:
СН²=СД²-ДН²=25²-7²=625-49=576;
СН=√576=24см. Мы нашли
высоту СН=МТ=АВ=диаметру=24см. Поэтому АВ, делясь в точке касания делится пополам на равные отрезки, которые равны радиусу. r=24÷2=12см
Поэтому: КВ=ВМ=АК=АТ=12см.
Теперь сложим отрезки оснований между собой и получим величины оснований трапеции:
ВС=12+9=21см
АД=12+16=28см
Теперь найдём площадь трапеции зная высоту и оба основания по формуле:
S=(ВС+АД)/2×СН=(21+28)/2×24=
=49×12=588см²