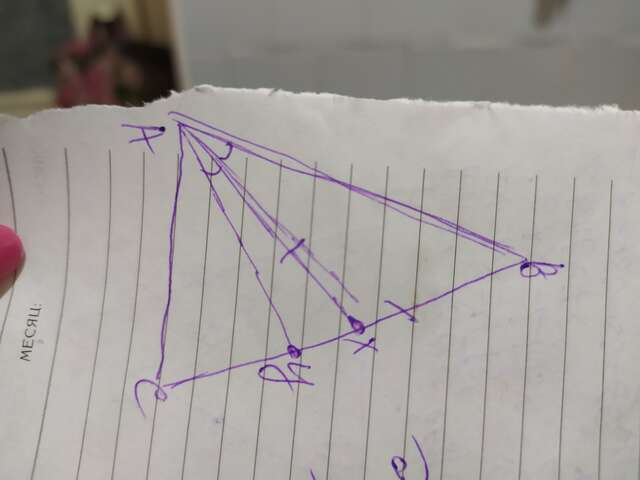
Ответ: АУ=6см
Объяснение: рассмотрим ∆АВХ. Он равнобедренный. По условиям АХ=ВХ и так как АХ=4√3, то ВХ=4√3см
Теперь рассмотрим ∆АВС.
Также по условиям ∆АВС- равнобедренный, поскольку АВ=ВС. Зная, что угол АСВ=75°, то угол ВАС, тоже будет 75°; угол АСВ=углу ВАС=75°
Теперь, зная 2 угла при основании, мы можем найти угол В.
Угол В=180-75-75=30°; угол В=30°
Так как ∆АВС равнобедренный, то угол ВАХ=углу УАХ=30°
Зная по условиям, что угол ВАХ=углу УАХ, и так как то они будут каждый по 30°. Теперь рассмотрим ∆САУ. Найдём в нём угол САУ. Зная что угол А=75°, то угол САУ=75-30-30=15°;
Угол САУ=15°. Теперь найдём в этом же треугольнике угол АУС, зная два угла: 180-75-15=90°; угол АУС=90°- это прямой угол, значит ∆САУ-прямоугольный. Теперь рассмотрим ∆АХУ. АУ в нём является стороной, образующей прямой угол, поэтому этот треугольник тоже прямоугольный. В нём катет ХУ лежит против угла 30°, поэтому ХУ= половине гипотенузы=4√3/2=2√3см;
ХУ=2√3. Так как в ∆АХУ мы нашли две стороны, тогда по теореме Пифагора найдём искомую АУ:
АУ=(4√3)²-(2√3)²=√(16×3)-√(4×3)=
=√(48-12)=√36=6см; АУ=6см