У прямокутному трикутнику висота яка опущена з вершини прямого кута дорівнює 3 см а...

Ответ:

$4{\sqrt{3} }$ см

Объяснение:

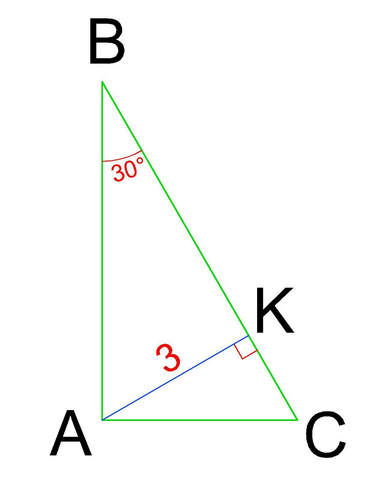
Побудуємо прямокутний ΔАВС, з висотою АК=3 см і гострим ∠В=30°.

І варіант рішення:

1) Розглянемо прямокутний ΔКВА.

Гіпотенуза АВ=АК/sin(B) ⇒ АВ=3/0,5=6 (см)

Катет ВК=АК/tg(B) ⇒ BK=3√3 (см)

2) Трикутники АВС, КВА та КАС подібні між собою (за гострим кутом як прямокутні трикутники). Тому

$\frac{BC}{AB} =\frac{AB}{BK}\Rightarrow BC=\frac{AB^2}{BK} \Rightarrow\\BC=\frac{6^2}{3\sqrt{3} } =\frac{12}{\sqrt{3} } =4\sqrt{3} (cm)$

ІІ варіант рішення:

1) Розглянемо прямокутний ΔКВА.

Гіпотенуза АВ=АК/sin(B) ⇒ АВ=3/0,5=6 (см)

2) Розглянемо прямокутний ΔКАС.

В ньому ∠С=180°-90°-∠В=60°.

Гіпотенуза АС=АК/sin(С) ⇒ АС=3*2/√3=6/√3 (см)

3) Розглянемо ΔАВС.

Гіпотенуза $BC=\sqrt{AB^2+AC^2} \Rightarrow BC=\sqrt{6^2+\frac{6^2}{3} } =\sqrt{36+12} =4\sqrt{3} (cm)$