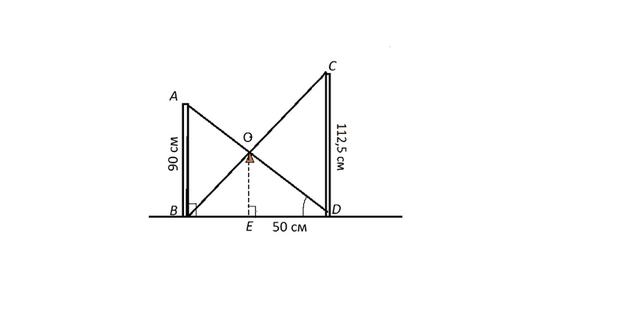
Для проведения одного из этапов соревнования "Смелые и ловкие" были установлены вертикально два шеста АВ и СDразной длины на некотором расстоянии друг от друга. Концы А и D, В и С соединены веревками, а в точке пересечения веревок прикреплен колокольчик. Если участник проползал между верёвками так, что колокольчик не звенел, то команде присуждали одно очко. На какой высоте ( в см) был подвешен колокольчик, если АВ=90 см, СD=112,5 см и ЕD=50 см?
Рассмотрим рисунок.
В треугольнике АВD расстояние от колокольчика до земли отсекает подобный ему треугольник ОЕD.
Оба треугольника прямоугольные, т.к. шесты установлены вертикально, а расстояние от О до земли измеряется перпендикуляром.
Пусть ВЕ будет х.
Составим уравнение с отношением соответственных сторон.
АВ:ОЕ=ВD:ЕD
90:ОЕ=(х+50):50
Произведение средних членов пропорции равно произведению крайних ее членов.
90*50=ОЕ(х+50)
ОЕ=4500:(х+50)
В треугольнике ВСD прямая ОЕ также отсекает подобный ему треугольник ВОЕ.
Составим пропорцию:
СD:ОЕ=ВD:ВЕ
112,5:ОЕ=(х+50):х
112,5х=ОЕ(х+50)
ОЕ=112,5х:(х+50)
ОЕ в обоих треугольниках одно и то же.
Приравняем его значения.
4500:(х+50)=112,5х:(х+50)
Умножив обе части уравнения на (х=50), избавимся от дроби.
112,5х=4500х=40 см
Найдем ОЕ из уравнения АВD, подставив в него найденное значение х: ОЕ=4500:(40+50)
ОЕ=50 см