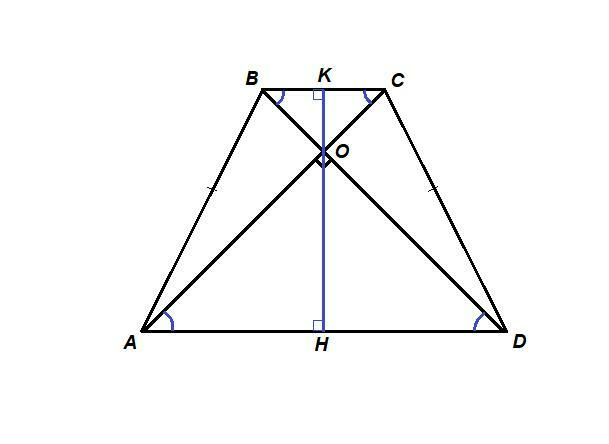
Ответ:
225 см²
Объяснение:
АВ = CD так как трапеция равнобедренная,
∠ВАD = ∠CDA как углы при основании равнобедренной трапеции,
AD - общая сторона для треугольников ВАD и CDA, ⇒
ΔВАD = ΔCDA по двум сторонам и углу между ними,
значит ∠CAD = ∠BDA.
Тогда ΔAOD равнобедренный прямоугольный.
ΔСОВ подобен ему по двум углам (∠OBC = ∠ODA как накрест лежащие при пересечении AD║BC и секущей BD, а углы при вершине О прямые), значит ΔСОВ тоже равнобедренный.
Проведем высоту трапеции КН через точку пересечения диагоналей.
Для равнобедренных треугольников AOD и ВОС отрезки ОН и ОК - высоты и медианы, а в прямоугольном треугольнике медиана, проведенная к гипотенузе, равна ее половине:
КО = ВС/2
НО = AD/2, ⇒
KH = (AD + BC)/2 = (18 + 12)/ 2 = 15 см,
тогда площадь трапеции:
S = (AD + BC)/2 · KH
S = (18 + 12)/ 2 · 15 = 15 · 15 = 225 (см²)
Полезно запомнить:
Если в равнобедренной трапеции диагонали перпендикулярны, то ее высота равна полусумме оснований или средней линии.