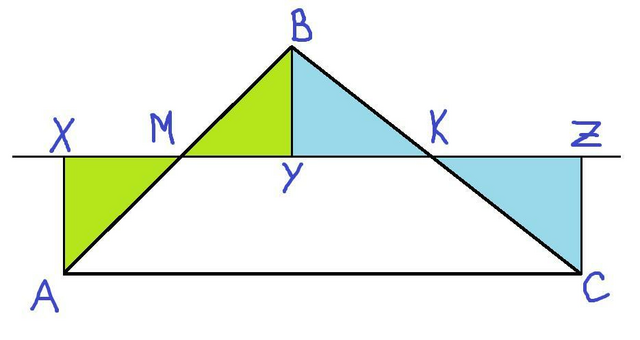
Так как нужно доказать, что вершины треугольника равноудалены от прямой МК, то проведем перпендикуляры к этой прямой из вершин треугольника: АХ, BY и CZ (расстояние от точки до прямой есть перпендикуляр).
Рассмотрим образовавшиеся треугольники АХМ и BYM. Они прямоугольные по построению. АМ=ВМ, так как по условию М - середина АВ. Углы АМХ и ВМY равны, так как они вертикальные. Значит, треугольники АХМ и BYM равны по гипотенузе и острому углу. В равных треугольниках против равных углов лежат равные стороны. В частности, против равных углов АХМ и BYM лежат равные стороны АХ и ВY.
Аналогично, рассмотрим треугольники ВYK и CZK. Они прямоугольные по построению. BK=CK, так как по условию K - середина ВC. Углы BKY и CKZ равны, так как они вертикальные. Значит, треугольники ВYK и CZK равны по гипотенузе и острому углу. Против равных углов BKY и CKZ лежат равные стороны ВY и CZ.
Итак, с одной стороны АХ=ВY, с другой стороны ВY=CZ. Значит, АХ=ВY=CZ. Это и есть расстояния от вершин треугольника до прямой МК. Значит, вершины треугольника равноудалены от прямой МК.