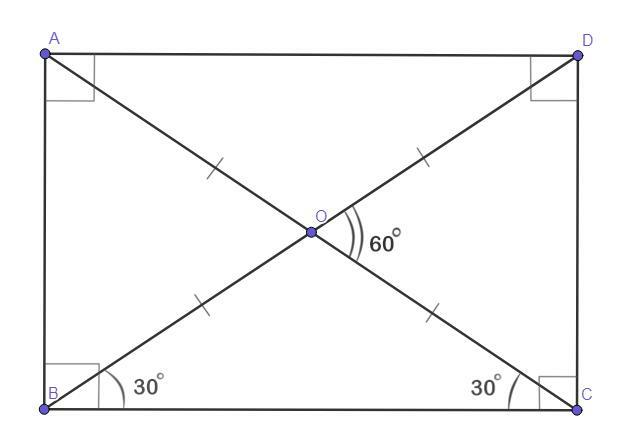
Чертёж смотрите во вложении.
Дано:
Четырёхугольник ABCD - прямоугольник.
DB - диагональ = 20.
∠DBC = 30°.
Найти:

Решение:
Проведём ещё одну диагональ АС. Точку пересечения АС и DB назовём О.
Прямоугольник - это тоже параллелограмм. Диагонали параллелограмма точкой пересечения делятся пополам. А так как ещё по свойству прямоугольника равны, то ВО = OD = AO = OC. Следовательно, ΔВОС - равнобедренный.
Рассмотрим ΔВОС - равнобедренный (ВО и ОС - боковые стороны). ∠ОВС = ∠ОСВ = 30°, так как прилегают к основанию. Рассмотрим ∠ODC - внешний для ΔВОС - равнобедренный. Следовательно, равен сумме углов не смежных с ним. То есть, ∠ODC = ∠ОВС +∠ОСВ = 30°+30° = 60°.
Площадь четырёхугольника равна половине произведения его диагоналей и синуса угла между ними.
S (ABCD) = 0,5*AC*DB*sin (∠ODC)
sin (60°) = (√3)/2.
AC = DB = 20.
То есть -


Ответ: 100 (ед²).