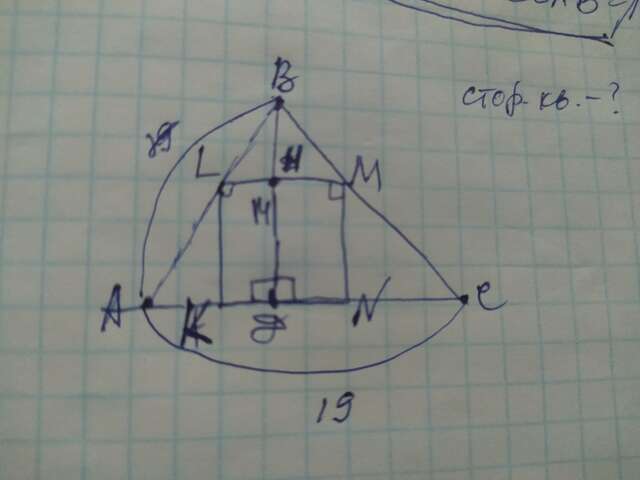
Ответ: сторона квадрата=266/33
Объяснение: обозначим точку пересечения высоты ВД со стороной LM точкой Н. Если сторона KN квадрата лежит на основании АС, то вторая его сторона LM, лежащая внутри ∆АВС будет параллельна LM. LM, так как она параллельна АС отсекает от ∆АВС ∆LBM подобный ∆АВС. Так как ∆LBM подобен ∆АВС, то их высоты ВД и ВН, стороны LM и АС будут пропорциональны:
LM/AC=ВН/ВД. Высота квадрата НД=сторонам квадрата. Пусть сторона квадрата=х, тогда ВН=14-х. Составим уравнение, используя пропорцию приведённую выше:
х/19=14-х/14
19(14-х)=14х
266-19х=14х
-19х-14х= –266
-33х= –266
х= –266/-33=266/33