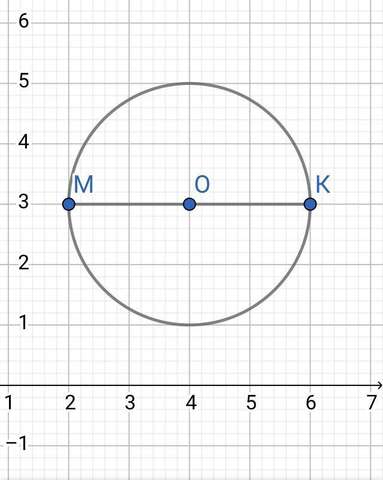
1) Найти радиус окружности.
МК = √((K(x) - M(x))² + (K(y) - M(y))²) = √((6 - 2)² + (3 - 3)²) = √16 = 4 ед.
Радиус окружности равен половине диаметра.
⇒ радиус окружности = МК/2 = 4/2 = 2 ед.
2) Найти координаты центра окружности.
Пусть О - центр окружности.
О(х) = (М(х) + К(х))/2 = (2 + 6)/2 = 4
О(у) = (М(у) + К(у))/2 = (3 + 3)/2 = 3
Итак, координаты О (4;3).
3) Написать уравнение окружности.
Уравнение окружности: (х - х₀)² + (у - у₀)² = R², где (х₀;у₀) - координаты центра окружности; (х;у) - координаты точки на окружности; R - радиус окружности.
⇒ уравнение данной окружности: (х - 4)² + (у - 3)² = 4
4) Окружность на картинке.