Відрізок BD - висота трикутника ABC, CD - 9 см, AD - 3 см. Кут С= 30 градусів. Яка...

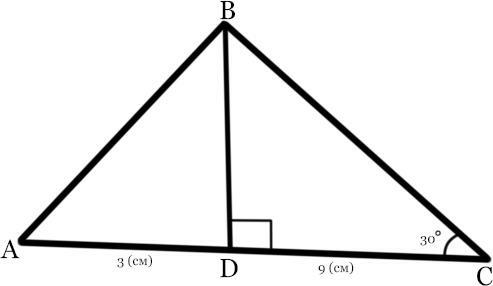
Дано :

ΔАВС.

BD - высота (∠BDC = 90°).

∠С = 30°.

CD = 9 (см).

AD = 3 (см).

Найти :

АВ = ?

Решение :

Рассмотрим ΔBDC - прямоугольный (так как ∠BDC = 90° по определению высоты треугольника).

$ctg(\angle DCB) = \frac{CD}{BD} \\\\ctg(60^{\circ} ) = \frac{9}{BD} \\\\\\frac{\sqrt{3} }{1} = \frac{9}{BD} \\\\BD*\sqrt{3} = 9\\\\BD = \frac{9}{\sqrt{3} }$

BD = 9/(√3) (см).

Рассмотрим ΔABD - прямоугольный.

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы (теорема Пифагора).

Следовательно -

$AD^{2} + BD^{2} = AB^{2} \\\\3^{2} + (\frac{9}{\sqrt{3} } )^{2} = AB^{2} \\\\9 + \frac{81}{3} = AB^{2} \\\\9 + 27 = AB^{2} \\\\AB^{2} = 36\\\\AB = 6$

АВ = 6 (см).

Ответ :

6 (см).