№1 (чертёж прилагается)
Дано:
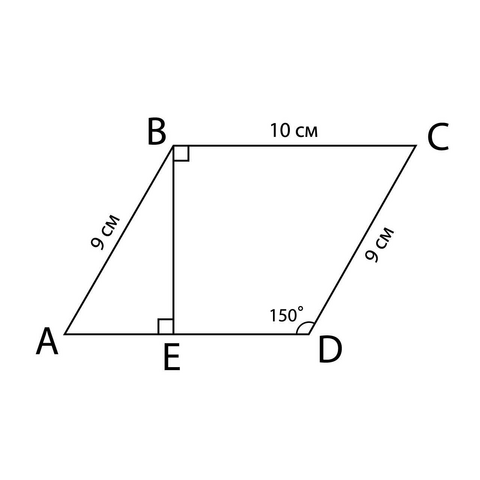
ABCD - параллелограмм.
∠ABC = ∠ADC = 150°
AB = CD = 9 см
BC = AD = 10 см
Найти: S параллелограмма ABCD
Решение:
∠BAD = ∠BCD = (360° - ∠ABC - ∠ADC) ÷ 2 =
= (360° - 150° - 150°) ÷ 2 = 60° ÷ 2 = 30° (сумма углов параллелограмма равна 360°)
Опустим высоту BE
Рассмотрим прямоугольный треугольник ABE:
∠A = 30° ⇒ BE = 1/2AB = 4,5 см (в прямоугольном треугольнике катет лежащий против угла в 30° равен половине гипотенузы)
S параллелограмма ABCD = AD × BE = 10 × 4,5 = 45 см² (площадь параллелограмма равна произведению его стороны на высоту опущенную к этой стороне)
Ответ: 45 см²
№2
Решение:
Рассмотрим треугольник CDE:
∠C = 180° - ∠D - ∠E =
= 180° - 45° - 90° = 45° (сумма углов треугольника равна 180°)
∠C = ∠D ⇒ ΔCDE равнобедренный ⇒
⇒ CE = DE = 4 см
Рассмотрим прямоугольный треугольник CBF:
∠B = 180° - 90° - 60° = 30° (сумма углов треугольника равна 180°)
Пусть AF = x
Тогда AB = 2x (в прямоугольном треугольнике катет лежащий против угла в 30° равен половине гипотенузы)
Найдём x:
x² + 4² = (2x)² (теорема Пифагора)
16 = 4x² - x²
3x² = 16
x² = 16/3
x = 4/√3 = (4√3)/3 см = AF
FE = BC = 3 см
AD = AF + FE + DE = (4√3)/3 + 3 + 4 =
= (4√3)/3 + 7/1 = (4√3 + 21)/3
S трапеции ABCD = (AD + BC)/2 × CE =
= ((4√3 + 21)/3 + 3)/2 × 4 =
= (4√3 + 30)/3 × 2 = (8√3 + 60)/3 (площадь трапеции равна полусумме оснований умноженной на высоту)
Ответ: (8√3 + 60)/3
№3 (чертёж прилагается)
Дано:
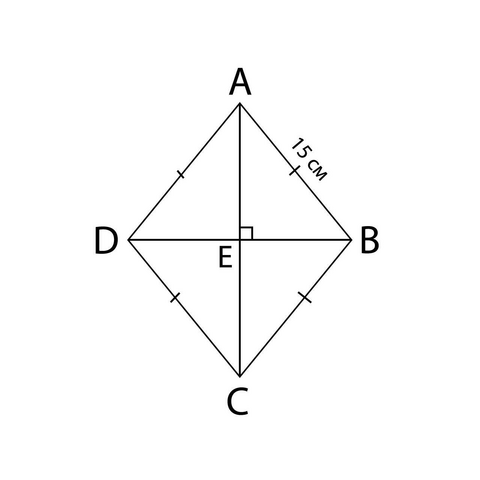
ABCD - ромб со стороной 15 см
AC = 24 см
Найти: S ромба ABCD
Решение:
Проведём вторую диагональ.
Диагонали ромба делят друг друга пополам ⇒
⇒ AE = CE = 1/2 AC = 24 ÷ 2 = 12 см
Рассмотрим прямоугольный треугольник ABE:
BE = DE = √(AB² - AE²) = √(225 - 144) =
= √81 = 9 см (теорема Пифагора)
BD = BE + DE = 9 + 9 = 18 см
S ромба ABCD = (AC × BD)/2 =
= (24 × 18)/2 = 24 × 9 = 216 см² (площадь ромба равна половине произведения его диагоналей)
Ответ: 216 см²