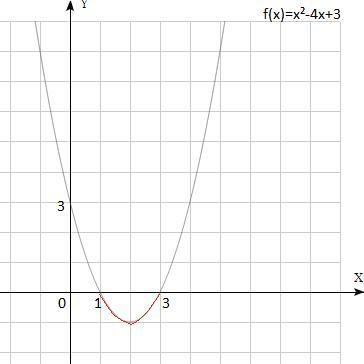
Постройте график функции f(x)=x²-4x+3. Пользуясь графиком, найдите;
1) промежуток возрастания функции ;
2) множество решений неравенства x²-4x+3≤0.
Объяснение:
f(x)=x²-4x+3 , парабола, ветви вверх.
f(x)=x²-4x+4-1,
f(x)=(x-2)²-1. Данную параболу можно получить сдвигом параболы у=х² на
- "2" единицы по ох вправо;
- "1" единицу по оу вниз..
А можно "не париться" и найти координаты вершины и точки пересечения с ох и оу (можно для более точного построения взять еще две точки, если хочется) : координаты вершины х₀=4:2=2 , у₀=-1.
Если х=0 , то у=3.
Если у=0 , то х=1, х=3.
1) Функция возрастает при х≥2 ( это там, где виртуальный человечек, двигаясь в положительном направлении, двигается вверх по параболе) .
2) Решением данного неравенства x²-4x+3≤0 будут те значения х на графике , у которых у≤0 ( часть параболы выделена красным цветом)⇒x∈[1 ;3]