Ответ:
Боковые стороны: a = 36 см
Основание: b = 32 см
Объяснение:
Пусть боковая сторона
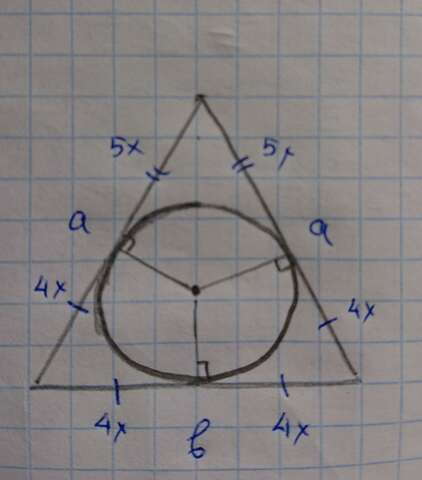
a = 5x + 4x = 9x
Для вписанной фигуры отрезки касательных от пересечения касательных до т. касания равны. Нам известно, что такой отрезок боковой стороны от основания до т. касания = 4x. Тогда длина основания b = 4x + 4x = 8x
Периметр равнобедренного треугольника
P = 2*a + b = 2*(5x + 4x) + (4x + 4x) = 2*9x + 8x = 26x = 104 см
x = 4 см
Боковые стороны: a = 5x + 4x = 9*4 = 36 см
Основание: b = 4x + 4x = 8*4 = 32 см