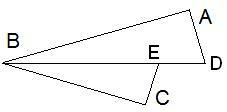
Дано, что BE — биссектриса угла CBA. AD⊥BAиCE⊥BC.
Найди BE, если AD= 9 см, BA= 12 см, CE= 7,2 см.
Сначала докажи подобие треугольников.
(В каждое окошечко пиши одну букву или число.)
∢A=∢ __ = __°
∢C __ D=∢DBA,т.к. __ E− биссектриса}⇒ΔCBE∼ΔABD, по двум углам (по первому признаку подобия треугольников).
BE= __ см.