Ответ:
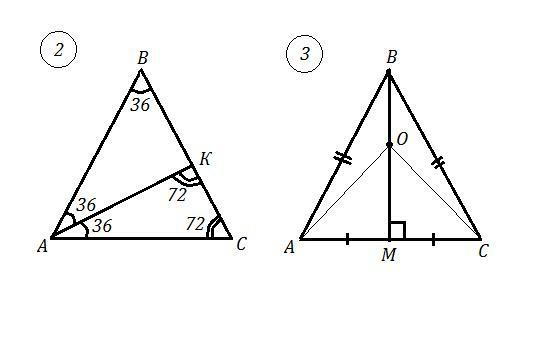
2) ΔАВС , АВ=ВС , ∠В=72°
ΔАВС - равнобедренный ⇒ ∠А=∠С=(180°-36°):2=72°
АК - биссектриса ⇒ ∠ВАК=∠САК=1/2*∠А=1/2*72°=36°
Так как ∠В=∠ВАК , то ΔАВК - равнобедренный.
Так как ∠САК=36° , ∠С=72° , то ∠АКС=180°-36°-72°=72° ⇒ ∠С=∠АКС , значит ΔАВК - равнобедренный.
3) ΔАВС - равнобедренный, АВ=ВС , АМ=СМ .
В равнобедренном треугольнике медиана ВМ является и высотой ⇒ ВМ⊥АС ⇒ ВМ - серединный перпендикуляр
Точка О принадлежит ВМ.
Любая точка , равноудалённая от концов отрезка, лежит на серединном перпендикуляре к этому отрезку. Значит, АО=СО .
Тогда ΔАОМ=ΔСОМ по трём сторонам (АМ=СМ по условию, МО - общая сторона , АО=СО) .