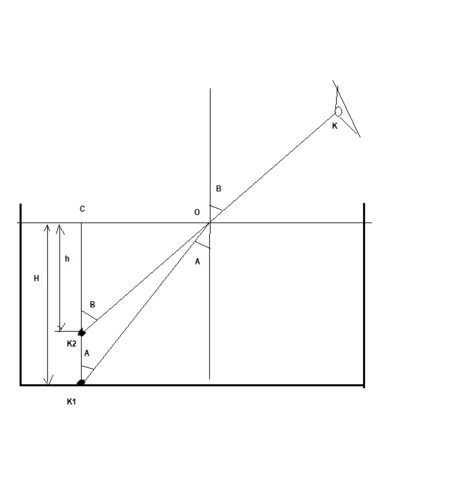
Начнем с того , что мы видим предметы в отраженном свете.
Точка К1(камень) находится на дне водоёма. Луч света , отражаясь от К1 попадает в точку раздела двух сред O и, преломившись, попадает в глаз наблюдателя – т. К. Глаз проецирует т.К в т.К1, и глубина водоёма нам кажется равной h.
Из рисунка видно, что кажущаяся глубина водоёма h зависит от истинной глубины H и от угла наблюдения В. Выразим эту зависимость математически:
Из треуг.(К1ОС) и треуг.(К2ОС) имеем:
H=OC/tgA ; h=OC/tgB
Приравняв ОС получим отношение h=HtgA/tgB=H(sinAcosB)/(cosAsinB) (1)
По известной формуле n=sinB/sinA
Подставим n в (1)
H=h √(n^2-sinB^2) /cosB= h√[(n^2-sinB^2)/ (1-sinB^2)] (2)
Водоём нам кажется мельче, чем он есть на самом деле.
Чем больше B – угол, под которым мы смотрим в водоём на предмет, тем меньше нам кажется глубина, на которой он находится. Следовательно, истинное положение предмета более искажено.
Глубина H будет казаться максимальной при B = 0°.
Тогда sinB= sin 0° = 0. Подставим в (2)
H= h√[(n^2-0)/ (1-0)] = 3√1.33^2= 3*1.33= 3.99 м = 4 м
Ответ = 3.99 м = 4 м