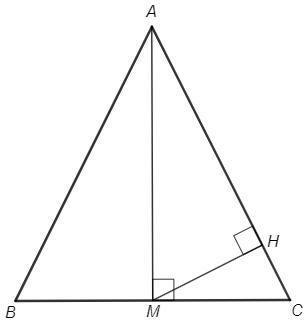
Равнобедренный треугольник, медиана является высотой, AMC=90
AMH~ACM (по двум углам, A - общий)
MCH~ACM (по двум углам, С - общий)
AMH~MCH
Площади подобных фигур относятся как квадрат коэффициента подобия.
S(AMH)/S(MCH) =(AM/MC)^2 =4/1
S(AMC)/S(MCH) =5/1
Медиана делит треугольник пополам.
S(ABC) =2 S(AMC) =10 S(MCH) =60