Дана окружность с центром O и её диаметры AB и CD. Определи периметр треугольника AOD,...

Question

Дана окружность с центром O и её диаметры AB и CD. Определи периметр треугольника AOD, если CB = 8 см, AB = 48 см. 1. Назови свойство радиусов окружности: все радиусы одной окружности имеют 2. Назови треугольник, равный треугольнику AOD = PAOD=

Answer 1

Ответ:

Объяснение:

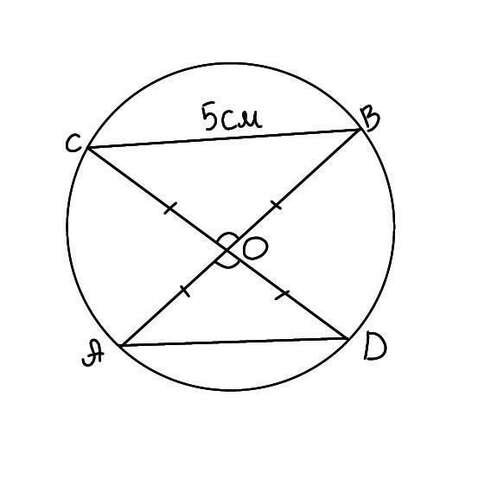
Рассмотрим ∆АОD и ∆СОВ. ОА = ОВ = СО = OD (радиусы одной окружности), углы СОВ и АOD равны, так как вертикальные, тогда ∆АОD = ∆СОВ по двум сторонам и углу между ними.

CO < CD в два раза, так как радиус меньше диаметра окружности. Поэтому, СО = ОВ = 50 см:2 = 25 см. P∆COB = 25 см+ 25см + 5 см = 55 см = P∆AOD.

1. Все радиусы одной окружности имеют равную длину.

2. AOD = COB.

3. Paod = 55 см.

Подробнее - на Znanija.com - znanija.com/task/36000458#readmore

---