Ответ:
Функция убывает на каждом из промежутков  и
и  .
.
Промежутков возрастания нет.
Точек экстремума и экстремумов функции нет.
Объяснение:

Область определения функции:



Найдем производную:


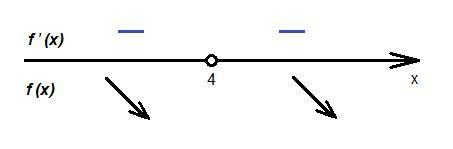
Знаки производной отметим на рисунке.
Так как производная отрицательна на каждом промежутке, то
функция убывает на каждом из промежутков  и
и  .
.
Промежутков возрастания нет.
Точек экстремума и экстремумов функции нет.