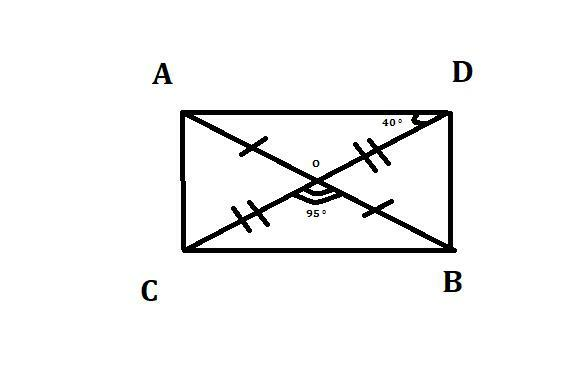
Решение:
Задача А).
Рассмотрим ∆AOD и ∆ВОС:
АО = ОВ, так как О - середина.
СО = OD, так как О - середина.
Вертикальные углы равны.
∠AOD = ∠COB, так как они вертикальные.
⇒ ∆AOD = ∆BOC, по 1 признаку равенства треугольников.
Задача Б).
Рассмотрим ∆AOD и ∆ВОС:
АО = ОВ, так как О - середина.
СО = OD, так как О - середина.
Вертикальные углы равны.
∠AOD = ∠COB, так как они вертикальные.
⇒ ∆AOD = ∆BOC, по 1 признаку равенства треугольников.
Ч.Т.Д.
⇒ ∠ADO = ∠OСВ, как накрест лежащие.
Если накрест лежащие углы равны, то прямые параллельны.
⇒ AD || BC
Сумма углов треугольника равна 180 °.
∠ОВС = 180 - (40 + 95) = 45 °
Ответ: 45 °