В правильной треугольной пирамиде MABC боковое ребро = 3√2 см, а высота пирамиды = √6...

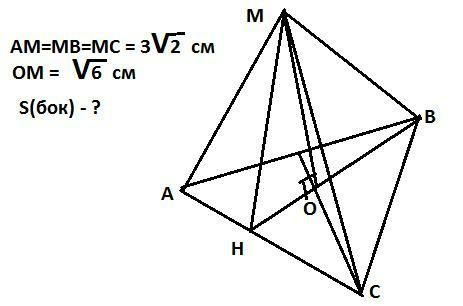
Ответ: S(бок) - 27 $\sqrt{3}$ см²

Объяснение:

Надо вычислить апофему и сторону основания.

1. Найдем апофему.

В правильной треугольной пирамиде, высота падает на точку пересечения медиан (в центр вписанной окружности, но в этом случае он совпадает с точкой пересечения медиан и это облегчает задачу).

Найдем отрезок медианы ОВ:

ОВ^2 = MB^2 - MO^2 = 18-6 =12

Тогда ОВ = 2 $\sqrt{3}$ см. Прямо отсюда видно, что ОМ =

В точке пересечения медиана делится в соотношении 2:1 начиная от вершины, поэтому ОВ = $\frac{2}{3}$ ВН, отсюда ВН = $\frac{3}{2}$ ОВ =

Значит отрезок ОМ = 4,5-3= $\sqrt{3}$ см

Из треугольника МОН апофема будет МН^2=OH^2 +OM^2 = 6+3 = 9

МН= 3 см

2. Найдем сторону. Медиана ВН делит сторону пополам (обозначим сторону а) . С учетом этого из прямоугольного треугольника АВН

a^2 - (a/2)^2 = BH^2 или $\frac{3a^2}{4} =$ 27, тогда а= 6 см

Площадь одной грани

S₁ = 0,5*a*BH = 0,5*6*3* $\sqrt{3}$ = 9

А всех трех

S(бок) = 3*S₁ = 3*9 $\sqrt{3}$ = 27