В прямоугольном треугольнике острый угол относится к внешнему углу, не смежному с ним как...

Question

В прямоугольном треугольнике острый угол относится к внешнему углу, не смежному с ним как 2:5. Найдите острые углы треугольника и его гипотенузу, если катет, лежащий напротив наименьшего острого угла равен 6 см

Answer 1

Ответ:

30°,  60°  12 см

Объяснение:

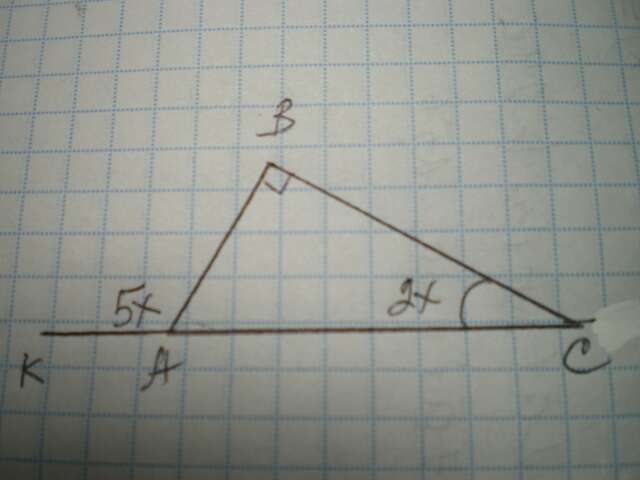
Внешний угол треугольника равен сумме внутренних углов, не смежных с ним.

Пусть ∠С=2х°, ∠КАВ=5х°, ∠В=90°,  тогда 2х+90=5х

3х=90;  х=30

∠С=30:2=60°;  ∠А=90-60=30°, т.к. сумма острых углов прямоугольного треугольника составляет 90°

Катет ВС лежит против угла 30°, следовательно, он равен половине гипотенузы АС

АС=2ВС=12 см.

---