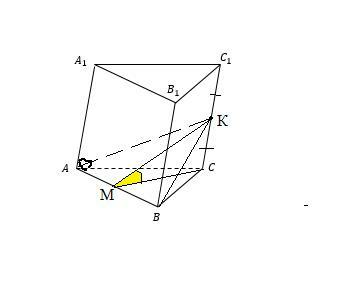
В правильной треугольной призме АВСА₁В₁С₁ через сторону АВ нижнего основания и середину ребра СС₁ проведено сечение , составляющие с плоскостью основания угол 30°. Найдите объем призмы, если боковое ребро равно 2b.
Объяснение:
V(призмы)= S(основания)*H, высота H -боковое ребро .
S(основания)=S(прав. треуг)= а²√3/4.
Пусть К-середина СС₁ , СК=2b:2=b .
Проведем СМ⊥АВ , тогда КМ⊥АВ по т. о трех перпендикулярах ⇒∠КМС-линейный угол двугранного между плоскостью сечения и основанием. ∠КМС=30°.
ΔКМС-прямоугольный , tg 30°=KC/CM или 1/√3=b/СМ , СМ=b√3 .
ΔСМВ-прямоугольный , sin60°=СМ/СВ , √3/2=b√3/СВ , СВ=2b.
S(прав. треуг)= (2b)²√3/4=b²√3.
V(призмы)= b²√3*2b=2b³√3 ( ед³)