Найдем производную функции.
Она равна:
(x^3)' + (-2x^2)' + (5)' = 3x^2 - 4x = x(3x-4)
Производная функции пересекает ось абсцисс в 2-х точках:
1) при x=0
2) при 3х-4=0, или x = 4/3
Получается, функция:
- возрастает на (-∞;0)
- убывает на (0; 4/3)
- возрастает на (4/3; +∞)
Значит, наименьшее значение функции будет равно f(4/3) = (4/3)^3 - 2*(4/3)^2 + 5 = 3 + 22/27
Для нахождения наибольшего сравним f(1) и f(5):
f(1) = 1 - 2 + 5 = 4
f(5) = 125 - 50 + 5 = 80
Значит, наибольшее значение на этом отрезке равно 80.
---
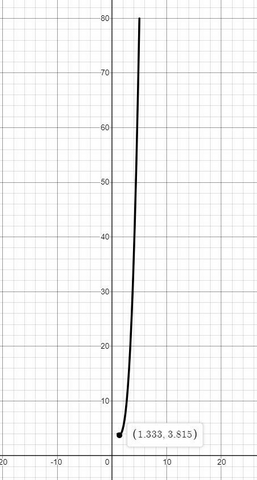
график функции в прикрепленном файле.