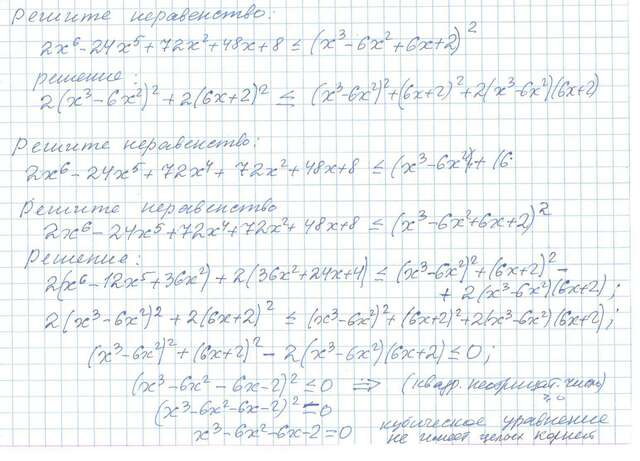znanija.com/task/37625801
решите неравенство :
2x⁶ -24x⁵+72x⁴ +72x²+48x +8 ≤ (x³ -6x³ +6x+2)
решение :
2x⁶ -24x⁵+72x⁴ +72x²+48x +8 ≤ (x³ -6x² +6x+2)²
2(x⁶ -12x⁵+36x⁴ +36x²+24x +4 ) ≤ ( (x³ - 6x²) + (6x+2) )² ;
2*(x⁶ -12x⁵+36x⁴ +36x²+24x +4 ) ≤ (x³ - 6x²)² + (6x+2)² +2(x³ - 6x²)(6x+2) ;
2*(x³ - 6x²)² +2*(6x+2)² ≤ (x³ - 6x²)² + (6x+2)² +2(x³ - 6x²)(6x+2) ;
(x³ - 6x²)² - 2(x³ - 6x²)(6x+2) +(6x+2)² ≤ 0 ;
( (x³ - 6x²) -(6x+2) )² ≤ 0 , но ( (x³ - 6x²) - 6x+2) )² ≥ 0 , поэтому
(x³ - 6x² - 6x - 2)² =0 ⇔
x³- 6x²-6x-2= 0 нужно решать полученное кубическое уравнение
x= ±1 , x = ±2 не являются корнем данного уравнения ,значит уравнение не имеет целых корней . Но кубическое уравнение имеет имеет хотя бы один действительный корень