Ответ:
Меньшее основание трапеции равно 4 см,
большее основание равно 36 см,
площадь трапеции равна 240 см²
Объяснение:
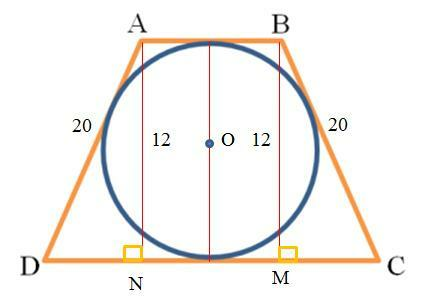
Как известно, в выпуклый четырехугольник ABCD, в нашем случае в трапецию (см. рисунок), можно вписать окружность тогда и только тогда, когда AB+CD=BC+AD, то есть
AB+CD=20+20=40 см
и, следовательно CD=40–AB.
Опустим из вершины A высоту AN, а из вершины B высоту BM. Площадь трапеции определяем через основания и высоту по формуле:
S=(AB+CD)•AN:2=40•12:2=40•6=240 см².
Теперь рассмотрим ΔADN с ∠AND=90°. По теореме Пифагора получаем:
DN²=AD²–AN²=20²–12²=(20–12)•(20+12)=8•32=8²•2²=16²,
то есть DN=16 см.
Так как треугольники ADN и BMC равны (4-ый признак: если катет и гипотенуза одного треугольника соответственно равны катету и гипотенузе другого треугольника, такие прямоугольные треугольники равны), то MC=DN=16 см. С другой стороны
CD=AB+DN+MC=AB+16+16=AB+32.
Приравниваем выражения для CD:
AB+32=40–AB
и находим AB=4 см.
Тогда CD=40–AB=40–4=36 см.